Obtenção da Matriz Zbus de Forma direta

Fazer um estudo de faltas em sistemas de energia elétrica é essencial para um correto dimensionamento das proteções necessárias em cada elemento. Entretanto para calcular as correntes de falta é necessário obter a matriz Zbus do sistema, essa publicação mostra como essa matriz é encontrada de forma direta.

A matriz Zbus usualmente é encontrada invertendo a matriz Ybus em sistemas com poucos nós, porem o algoritmo de inversão passa a demandar um grande esforço computacional em casos maiores visto a quantidade de elementos, nesse tipo de cálculo também é necessário um recalculo de toda a matriz Ybus e uma nova inversão caso ocorra uma pequena mudança na topologia do sistema. Assim para essa publicação é mostrada outra forma de obter Zbus diretamente, adicionando ramo a ramo.

Inicialmente se adiciona um elemento ligado ao nó de referência, nesse caso entre as barras 1 e 0, a matriz Zbus fica então:

Se adiciona o elemento 5-1 de uma barra nova para a barra 1 existente, se altera a matriz Zbus de forma que se copia os elementos da barra existente que se quer anexar o elemento em uma nova linha e coluna e na diagonal principal é somado o elemento novo com a impedância Thevenin vista pela barra existente.

Da barra 5 é adicionado o elemento z52 no sistema, adicionando novamente uma nova barra a uma barra existente pelo mesmo processo:

Adicionando a barra 4 da mesma maneira:

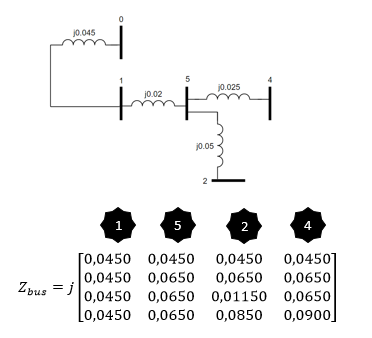
Para adicionar o elemento z24 é feito a adição do elemento entre duas barras existentes, a nova linha da matriz Zbus é a subtração das linhas das barras 2 e 4 e a nova coluna é a subtração das respectivas colunas, o novo elemento da diagonal principal é obtido pela soma dos thevenin observados por cada barra menos duas vezes a impedância z24 adicionada a impedância que se quer acrescentar. Entretanto ao realizar as operações descritas a matriz Zbus deixa de ter o tamanho correto para o sistema pois uma nova barra fictícia foi adicionada, então se aplica a redução de kron para excluir essa barra.

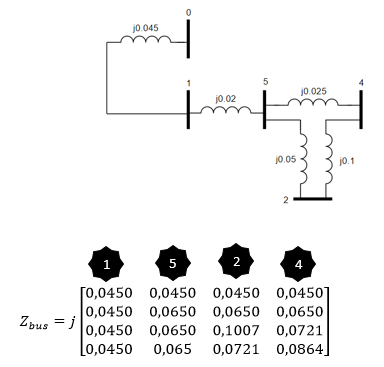
É adicionado então o elemento z43 da mesma maneira descrita anteriormente:

Por fim é adicionado o elemento shunt da barra 3 também adicionando uma barra p fictícia para que o equacionamento seja semelhante ao acréscimo de uma impedância de uma barra nova a uma barra existente, assim o elemento da diagonal principal é a soma da impedância thevenin visto na barra existente e a nova impedância. Para eliminar a barra fictícia é utilizada novamente a redução de Kron.

Vale ressaltar que a diagonal principal da matriz Zbus representa a impedância thevenin vista da barra em questão, ou seja a rede vista desde cada barra, entretanto os elementos fora da diagonal não representam o equivalente entre duas barras, e sim uma visão do sistema desde a barra i quando se injeta corrente na barra j no elemento Zij.