Curto-circuito trifásico

Para o desenvolvimento dessa atividade foram determinados todos os parâmetros necessários para o desenvolvimento das análises de curto-circuito trifásico. Isso inclui a aplicação de uma falta trifásica em todas as barras do sistema, como também a obtenção das correntes de falta e dos ramos, e as tensões das barras. Além disso, foi realizada uma variação do caso base, relacionada a inserção da uma carga de 400 MW e 150 Mvar na barra 2 do sistema.

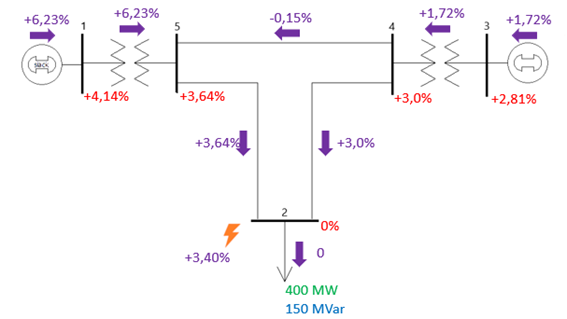
O circuito base utilizado para as análises é apresentado pela Figura 1. Sendo o sistema composto por cinco barras, dois geradores, dois transformadores, linhas de transmissão e uma carga, esta que inicia com valor zero (caso base).

Figura 1 - Caso base.

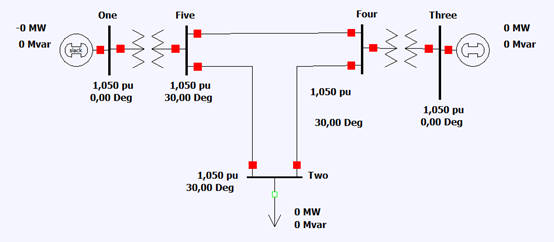
Analisando agora alguns casos implementados, é realizado primeiramente a variação para o sistema sem carga e com uma falta na barra 2. Como podemos observar pelo sistema ilustrado, temos que o gerador 2 é quem terá a maior contribuição para a corrente de curto com um valor de 11,18 pu, enquanto o gerador 1 é quem irá contribuir com a outra parcela, totalizando um valor de 18,44 para a corrente de falta na barra. Pode-se observar aqui também que os valores das tensões nas barras também diminuíram, de acordo com a passagem dessa corrente de grande magnitude pelo circuito.

Figura 2 - Falta na barra 2 sem carga.

Os resultados foram obtidos através da simulação no software PowerWorld, mas a obtenção dos valores pode ser realizada também de maneira analítica. Desta forma, de maneira didática será apresentado um método numérico para o cálculo das correntes (de falta e dos ramos) e da tensão nas barras do sistema base.

Para iniciar o método, deve-se realizar o levantamento da matriz Ybarra do sistema, pois através dela é que será possível obter os parâmetros que representam a topologia do sistema. Portanto, essa matriz foi retirada da simulação do Powerworld e seus valores estão disposta na Figura 3 abaixo.

Figura 3 - Matriz Ybarra.

Contudo, para o cálculo da variação das tensões é necessário da matriz Zbarra, que nada mais é do que a inversa da matriz admitância de barra. Dessa maneira, deve-se realizar a inversão da matriz Ybarra e a partir dos valores encontrados será possível calcular ΔV, neste caso para um curto-circuito na barra 2 do sistema.

Feito isso, os valores retirados da matriz impedância de barra são os relativos à coluna dois, isso porque a falta acontece na barra 2 e serão essas as impedâncias submetidas a corrente de falta If", conforme apresentado pelo equacionamento abaixo.

Onde If" será a tensão de falta (antes do curto-circuito) sobre a impedância de Thévenin, vista pelo ponto de falta. Sendo assim, substituindo a corrente de falta subtransitória na equação anterior, temos que as variações de tensões são obtidas através da formulação apresentada.

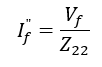
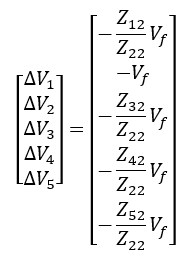
Agora com o valor de ΔV será possível calcular a tensão em todas as barras, neste caso para o curto trifásico na barra 2 do sistema. Da mesma forma que anteriormente, é apresentado o equacionamento para a obtenção dos valores e caberá ao leitor realizar a substituição dos parâmetros para encontrar os resultados, sendo isso realizado como forma de aprendizado e fixação.

Destaca-se que a Figura 2 serve como base para validação dos resultados encontrados pelo leitor, pois apresenta todas as tensões e correntes nos ramos. Sendo que este segundo parâmetro pode ser calculado através do equacionamento abaixo, onde a corrente Iij" é igual a tensão da barra “i” menos a da barra “j”, sobre a impedância do caminho entre essas duas barras. Ou seja, nessa equação não é utilizada a impedância da matriz Zbarra.

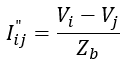
Já na próxima análise, temos a falta na mesma barra, só que agora com uma carga indutiva de 400 MW e 150 Mvar. Então, são apresentadas as variações em porcentagem das correntes e tensões do circuito, onde tanto a corrente de falta na barra 2 quanto as correntes de contribuição dos geradores aumentam, e as tensões nas barras diminuem também por conta da maior corrente de falta passando pelo sistema.

Figura 4 - Falta na barra 2 com carga.

Agora iremos apresentar mais um caso, sendo este o considerado mais crítico do sistema, pois para uma falta na barra 3 a corrente injetada pelo gerador 2 se configura como a maior corrente de falta vista em todas as simulações das barras, podendo de acordo com as limitações técnicas do gerador danificar o dispositivo por exceder o limite da corrente da máquina. Essa maior corrente é explicada também pela menor distância elétrica, pois no caminho da falta existe apenas a impedância síncrona do gerador 2 e que é de apenas 2,25%, então a impedância de Thévenin nesse ponto é a mais baixa e por conta disso a corrente de falta será a maior entre todos os casos.

Figura 5 - Falta na barra crítica sem carga.

Agora para o caso com a carga podemos observar, da mesma maneira que o comportamento anterior, em um aumento da corrente de curto-circuito, e consequentemente da contribuição dos dois geradores e também no aumento das tensões das barras, menos na barra de carga. Isso acontece porque a carga possui características indutivas, o que implica em um consumo de reativos e consequentemente leva a uma redução da tensão na barra de carga.

Figura 6 - Falta na barra crítica com carga.

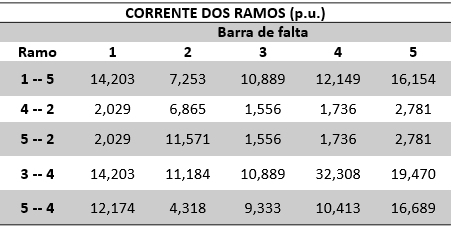
Analisando agora as correntes nos ramos na Tabela 1, temos que o maior valor encontrado se configura quando aplicamos uma falta na barra 4, aqui podemos perceber pela mesma análise anterior. Pois essa barra é a mais próxima da barra do gerador 2, ou seja, onde estava o ponto mais crítico do sistema. Desta forma, a distância elétrica será bastante pequena também, pois impedância de Thévenin enxergada será apenas a soma da impedância do gerador e do trafo.

Tabela 1 - Corrente nos ramos para faltas nas barras.

E agora na Tabela 2 são apresentadas as diferenças entre as correntes dos ramos com e sem carga. Através desses valores nós concluímos que para estudos de curto-circuitos, no cálculo da corrente de falta em sistemas de extra e alta tensão não existe a necessidade de considerar a carga no SEP, isso porque a sua contribuição é pequena quando comparada a ordem de grandeza da corrente de falta. Desta forma, para realizarmos o dimensionamento dos dispositivos de proteção essa aproximação da corrente de curto-circuito já se mostra satisfatória.

Tabela 2 - Diferença entre as correntes nos ramos com e sem carga.

De acordo com as análises realizadas, temos que quando são adicionadas cargas ao sistema a corrente de curto-circuito pode aumentar ou diminuir. Isso se dá por conta do acréscimo de IL nessa corrente subtransitória, como mostrado pelo equacionamento na Figura 7. Pode-se destacar que esse valor de IL é muito menor quando comparado ao outro termo.

Figura 7 - Equacionamento da corrente de falta subtransitória.